Math for Liberal Arts

DSST test prep for Math for LIberal Arts

Course Description

“What is mathematics? … It’s certainly not just a fixed body of knowledge, … its hidden tendrils pervade every aspect of modern life.” — Ian Stewart

The Math for Liberal Arts DSST exam covers topics such as real number systems; sets and logic; metric system; conversions and geometry; algebra, graphs and functions (as applied to real life applications); linear systems and inequalities; exponents and logarithms including financial literacy and counting; probability theory and statistics. The use of a non-programmable calculator is permitted in this exam.

Exam Outline

The following is an outline of the content areas covered in the examination. The approximate percentage of the examination devoted to each content area is also noted.

I. Real Number Systems – 11%

  1. Real numbers: Natural Numbers, Integers, Rational Numbers, Irrational Numbers, The real number line. ( Percentages; Fractions and reducing fractions; conversion between decimal numbers and fractions; operations with fractions (including distributive property)
  2. Operations with real numbers and their properties (including the distributive properties)
  3. Prime and composite numbers; divisibility rules; prime factors of composite numbers
  4. Systems of Numeration: Place value or positional value numeration, Base 10 expanded forms; base 2 numbers; conversion between base 10 and base 2; (Including Roman Numerals)
  5. Rules of exponents including rational exponents
  6. Scientific notation

II. Sets and Logic – 16%

  1. The Nature of Sets
  2. Subsets and Set Operations, (set-builder notation; roster form, using sets to solve problems)
  3. Using Venn Diagrams to Study Set Operations
  4. Infinite Sets
  5. Simple and compound statements; qualifiers “and” and “or” and their symbols; conjunction and disjunction; conditional and biconditional statements including Qualifiers
  6. Truth value of a compound statement including Truth Tables
  7. Types of Statements ( Negations of Conditional Statements and De Morgan’s Laws)
  8. Logical Arguments including Euler Circles

III. Metric system, conversions and geometry – 12%

  1. Introduction to metrics and U.S. customary unit systems
  2. Conversions between metric and U.S. customary unit systems, including Dimensional Analysis
  3. Properties of lines and angles
  4. Perimeter and area of 2D geometric objects e. Area, Surface area and volume of 3D solid objects

IV. Algebra, graphs and functions (as applied to real life applications)– 11%

  1. Order of operations
  2. Simplifying expressions; equations with one variable; proportion problems
  3. Evaluation of formulas
  4. Graphs of linear equations in the rectangular coordinate system
  5. Functions including polynomials (not to include rational, exponential and logarithmic Functions)

V. Linear Systems and Inequalities – 8%

  1. Solving Linear Equations including applications and systems
  2. The Rectangular Coordinate System and Linear Equations in Two Variables
  3. Graphing and solving Linear inequalities
  4. Graphing and solving systems of inequalities

VI. Exponents and Logarithms including Financial Literacy – 22%

  1. Properties of Logarithms
  2. Logarithmic and Exponential Functions
  3. Simple InterestCompound Interest
  4. Compound Interest
  5. Installment Buying
  6. Student Loans and Home Buying
  7. Investing in Stocks and Bonds

VII. Counting, Probability Theory and Statistics – 20%

  1. Fundamentals of Probability including the Counting Principle
  2. Permutations and Combinations
  3. Events Involving Not and Or
  4. Odds and Conditional Probability
  5. Mean, Median and Mode
  6. Range, Variance and Standard Deviation
  7. Graphical representation (including Bar graph, pie chart, histogram, line graph, scatterplots etc.)

Sample Questions

All test questions are in a multiple-choice format, with one correct answer and three incorrect options. The following are samples of the types of questions that may appear on the exam.

1. Heidi and Oliver are planning to buy a bedroom furniture set that costs $4,100 plus 6% taxes. They would like to apply for a 0% APR store credit card on purchases for 10 months. How much money do they need to pay in equal installments monthly for the next 10 months such that they will be able to pay off the bedroom furniture set before the 0% APR offer expires?

  1. $43.46 per month.
  2. $385.40 per month.
  3. $410.00 per month.
  4. $434.60 per month.

2. An electronics store sold 1,500 computers and smartphones in a month. Out of the total number of consumers who purchased these items, 2% bought a computer and a smartphone, while the others bought only a computer or a smartphone. If 1,206 consumers bought smartphones, how many people bought computers?

  1. 324 consumers.
  2. 2.16% of all consumers.
  3. 19.6% of all consumers.
  4. 294 consumers.

3. If the figure below is constructed out of two semicircles and a square, what is the area of the whole figure? (Round to the nearest tenth of a meter squared)

  1. 37.3 m2
  2. 50.1 m2
  3. 64.3 m2
  4. 149.1 m2

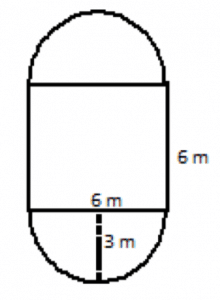
4. Write a variable expression for the area of a square whose side length is (x + 8) units.

  1. x2 – 16x + 64 square units
  2. x2 + 16x + 64 square units
  3. x2 + 16x – 64 square units
  4. x2 + 64x + 16 square units

5. The population growth of an animal species is described F(t) = 320 log(4t + 4), where t is the number of months since the species was introduced. Find the population of this species 8 months after the species is introduced to an area. Round to the nearest whole number.

  1. -1
  2. 320 
  3. 498
  4. 1147

 6. Find the mode for the following data: 12, 12, 12, 14, 16, 18, 20, 22, 25, 25, 29, 33, 37, 37, 39.

  1. 12 
  2. 25 
  3. 37 
  4. 39

7. The function f(x) = 2.4 + 8 ln x, given in centimeters, models the height of a certain animal species where x is the number of days the animal has been alive. Determine the height of the animal after it has been alive for 16 days.

  1. 15.47 cm 
  2. 12.03 cm
  3. 15.89 cm
  4. 24.58 cm

8. Determine the logical conclusion for the arguments below:

Some college students join school sponsored clubs. No school sponsored clubs endorse bullying.

  1. Some school sponsored clubs have college student members.
  2. All school sponsored clubs prevent bullying.
  3. Some college students do not endorse bullying.
  4. Bullies are able to join school sponsored clubs.

Answers to sample questions:

1-D,   2-A,  3-C,  4-C,   5-A,   6- A,   7-D,   8-C

Sign Up Now

Backed by Our Money-Back Guarantee!

Quick Facts

Here’s what you need to know about this exam:

  • 80 questions
  • Time Limit: 2 hours
  • Course Equivalent: Math for Liberal Arts
  • Recommended Credit: 3 Semester Hours

DSSTPrep
A Making educationPossible company

Account

Terms of USe

About DSST Prep

DSSTPrep
10900 Research Blvd Ste 160C PMB 1356           Austin, TX 78759

support@dsstprepcourses.com

 

Facebook-f

© 2023 All rights reserved

PARTNERS 

SPEEDYPREP | DSST PREP | PATRIOT EDUCATION 

military friendly colleges | veterans friendly college